3.2.7 Process Tensor
This button is used to start the tensor estimation. There are a number of options available to the user, as seen in the opt button to the right of the process tensor button. More options will be available with future releases of the software.
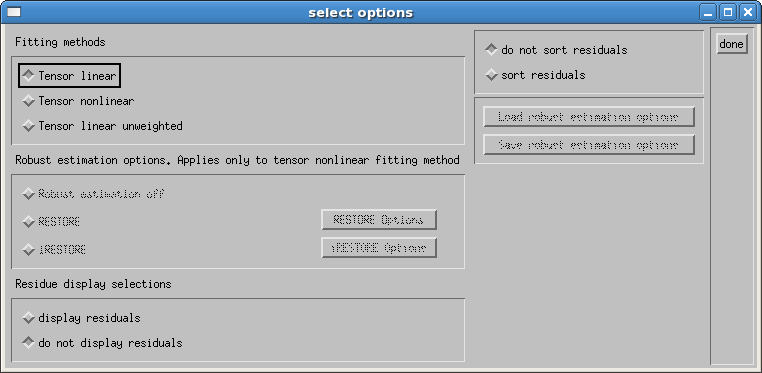
The first options allow you to choose the tensor fitting algorithm. There are three options1:
- tensor linear
- tensor nonlinear
- tensor linear unweighted
The default value is linear because it is the fastest algorithm, however, the use of the non-linear algorithm is highly recommended as it provides a more accurate estimate of the tensor.
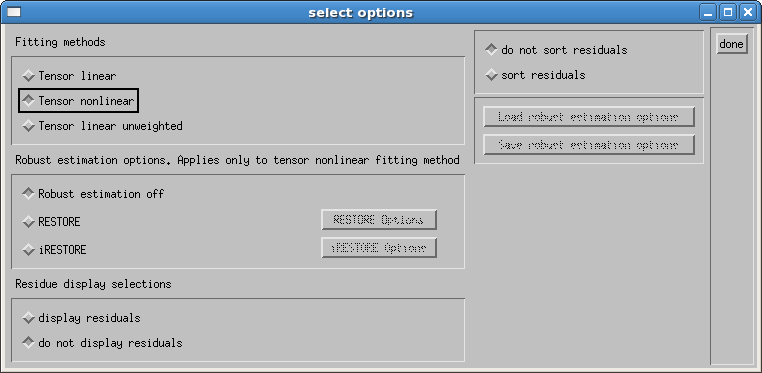
Robust estimation options are either RESTORE2 or informed RESTORE (iRESTORE)3, and are only available with the tensor nonlinear option. Default is "off". We recommend using the automated noise estimation option when using RESTORE or iRESTORE robust tensor fitting.
RESTORE and iRESTORE have additional user defined options. See the following pages for details.
The Residue display selections allows the user to display a histogram of the residuals of the tensor fitting. This can help to indicate to the user if there is a problem with the fitting. Default value is do not display residuals. The final two options allow the user to adjust the display of the histogram by choosing whether or not to sort the residuals.
When the appropriate options have been selected, click done, then click the process tensor button. This will fit the tensor, calculate the eigenvalues and eigenvectors, and then derive all the tensor derived metrics. This will create a new .list, .bmtxt and .path file for your data, with _L0 appended to the name for linear fit, _N1 for non-linear fit, _LU for unweighted linear fit, _R1 for RESTORE robust fit, and _iR1 for informed RESTORE robust fit. It will also create a directory with the same name appended with _SAVE. This SAVE directory contains the tensor derived metric images in either analyze or nifti format, depending on the setting in your configuration file.
References
- Basser, P.J., Mattiello, J., and LeBihan, D. (1994) Estimation of the effective self-diffusion tensor from the NMR spin echo. J Magn Reson B 103:247-254.
- Chang, L.C., Jones, D.K., and Pierpaoli, C. (2005) RESTORE: Robust estimation of tensors by outlier rejection. Magn Reson Med. 53:1088-1095.
- Chang, L.C., Walker, L., Pierpaoli, C., (2012) Informed RESTORE: A Method for Robust Estimation of Diffusion Tensor from Low Redundancy Datasets in the Presence of Physiological Noise Artifacts. Magn Reson Med. 68(5):1654–1663.
